Binary Search Tree

BST的查找，插入和删除的时间复杂度平均为$log_2^n$。

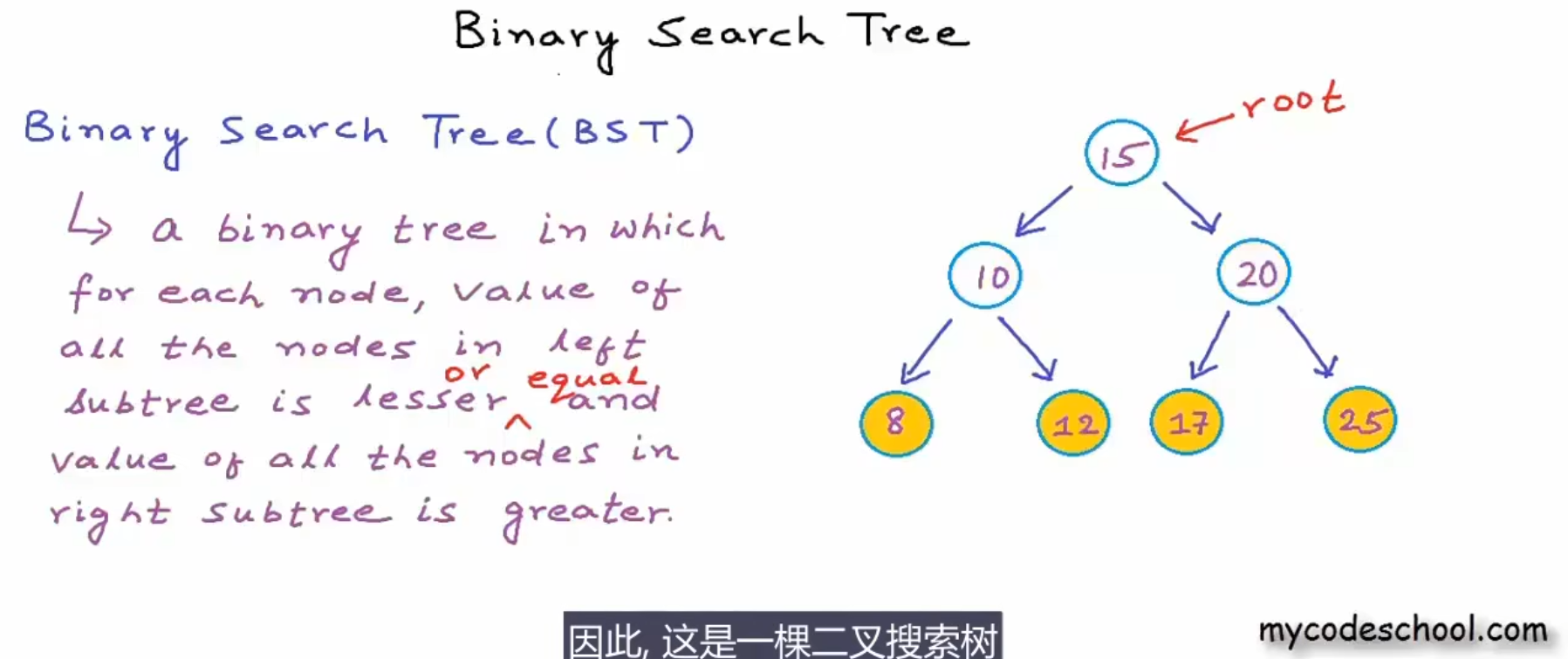
Definition

对于二叉树的每一个节点 ，其对应左子树中的所有节点中的值必须小于等于它自己，并且右子树中所有节点中的值必须大于它自己。不需要考虑leaf nodes
image-20250315153051106

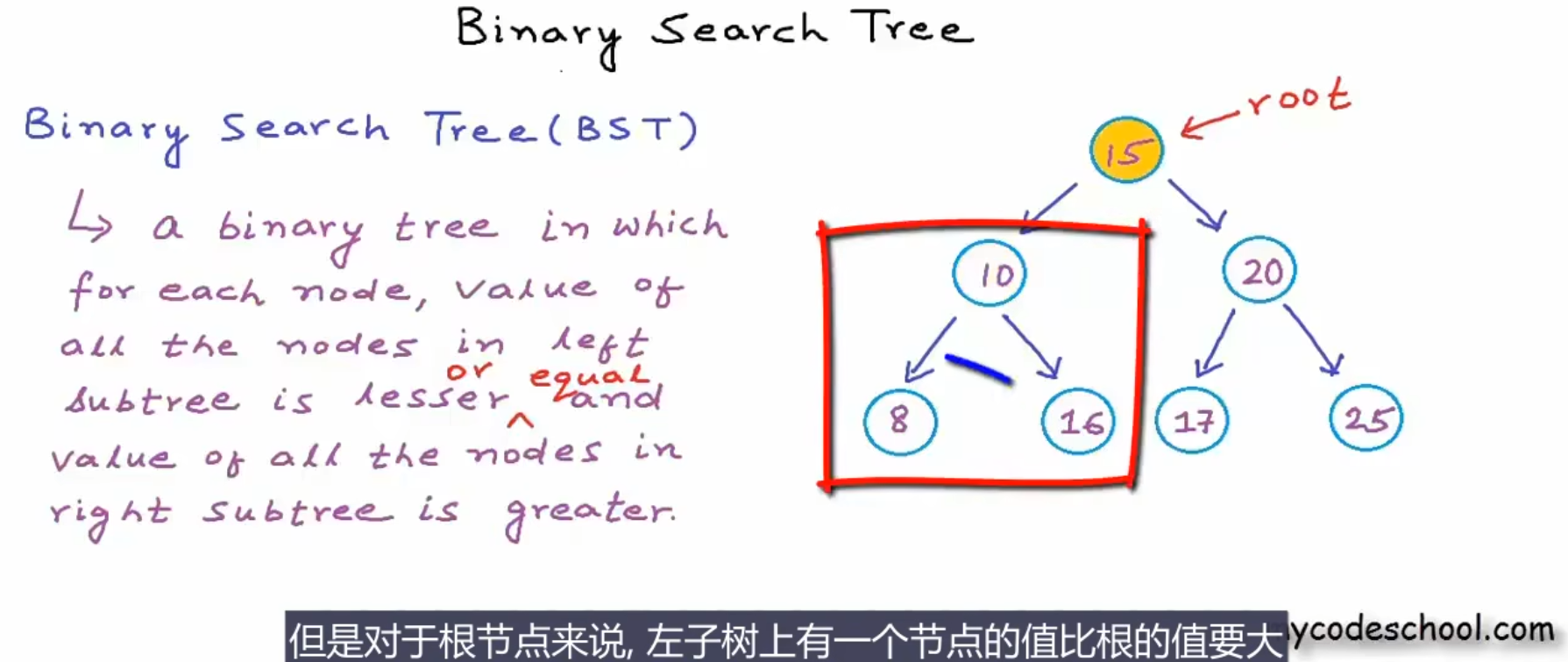
如下图所示，对于根节点来说左子树上有一个节点的值比根大，因此不满足二叉搜索树的条件。

image-20250315153236865

Operation

Search(x)

首先提及二分查找的思路：
二分查找通过比较目标值与数组中间元素的大小，决定继续在左半部分或右半部分进行查找。具体步骤如下：

  1. 找到数组的中间元素。
  2. 如果目标值等于中间元素，则查找成功。
  3. 如果目标值小于中间元素，则在左半部分继续查找。
  4. 如果目标值大于中间元素，则在右半部分继续查找。
  5. 重复上述过程，直到找到目标值或搜索范围为空。
  • 初始搜索范围是 n。
  • 第一次查找后，搜索范围缩小为 n/2。
  • 第二次查找后，搜索范围缩小为 n/4。
  • 依此类推，第 k 次查找后，搜索范围缩小为 n/2k。

当搜索范围缩小到 1 时，查找结束，即：

解这个方程，得到：

BST的搜索与之类似

search(x)

image-20250315154533277

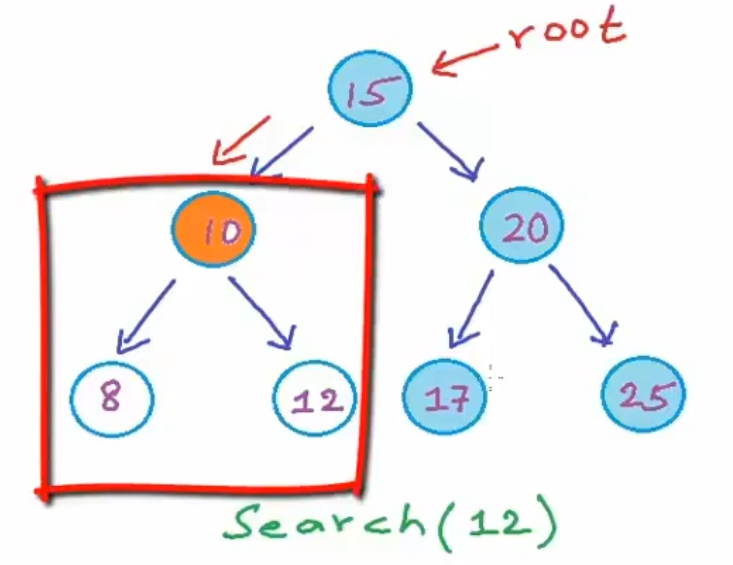
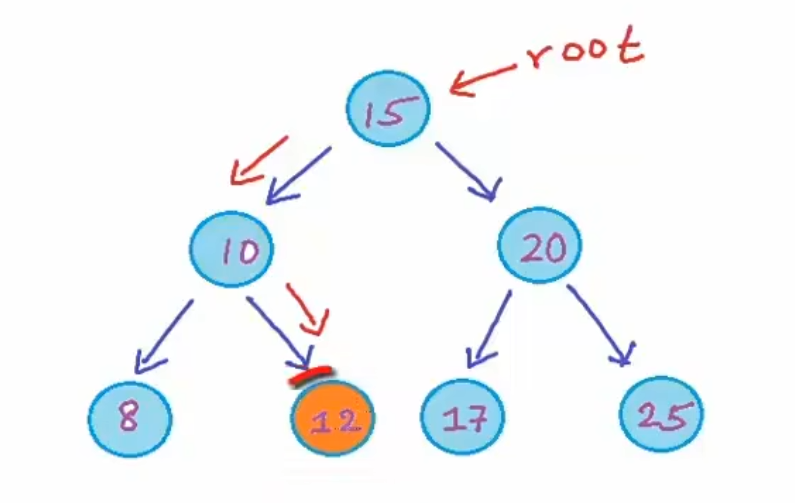
  • 比如说，由上图，我们准备搜索12，从根开始与待搜索的值进行比较，发现12小于根节点的值，因此需要到左边的子树中进行搜索，因为BST中的左子树中的只都更小，右子树中的值都更大，此时来到左子树中。

image-20250315154924224

  • 只需要看左子树中的节点，搜索空间减少了一半，此时比较10，发现更大，因此来做10这个节点的右子树，此时搜索空间只剩下一个节点，我们再一次比较这个节点的值，然后找到了匹配。

image-20250315155150846

  • 因此在二叉搜索树中查找一个元素基本上就是这样进行遍历，这样进行遍历在平衡的BST中的时间复杂度为$O(log_2^n)$，一棵树平衡的条件是，对于任何节点，左右子树的高度差不大于1。如上图就是一个平衡的，实际上是完美二叉树，所有节点均被填满

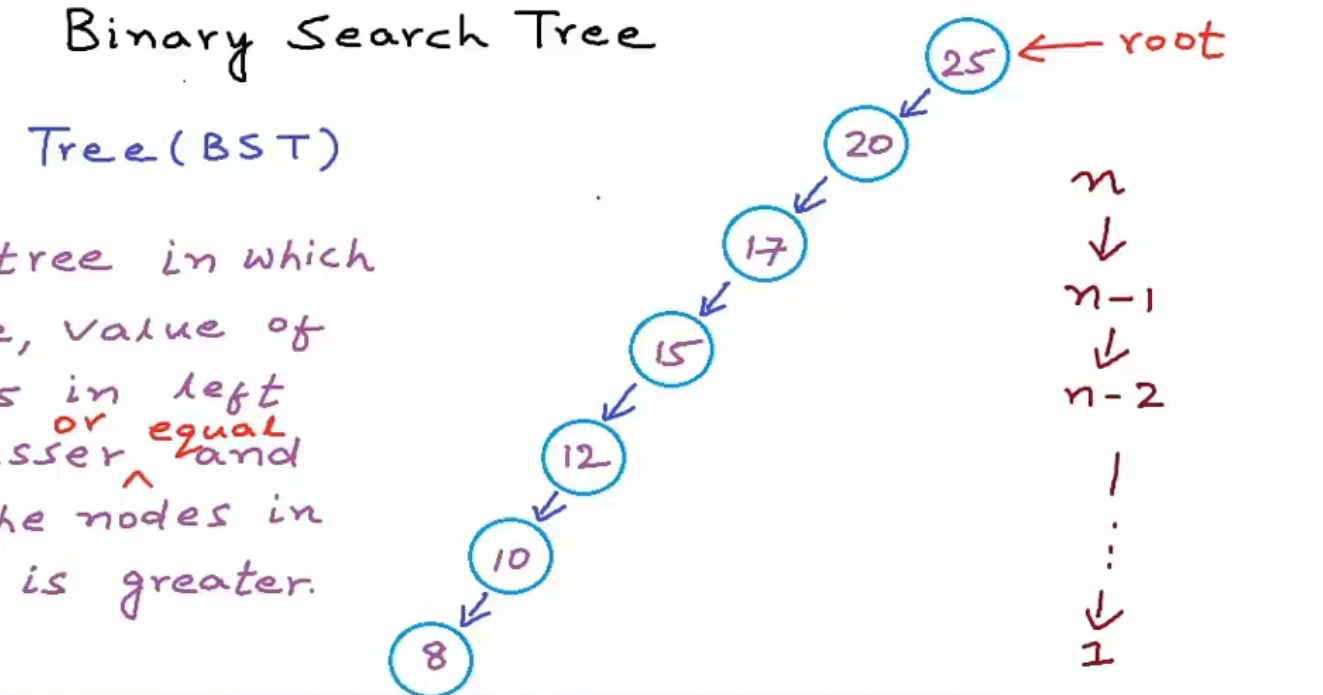
  • 对于最坏的情况，如下图二叉树是一颗不平衡的BST，如同一个链表一样，所有节点都没有右子树，每次搜索后搜索空间只会减少1，此时时间复杂度为O(n)

image-20250315155827126

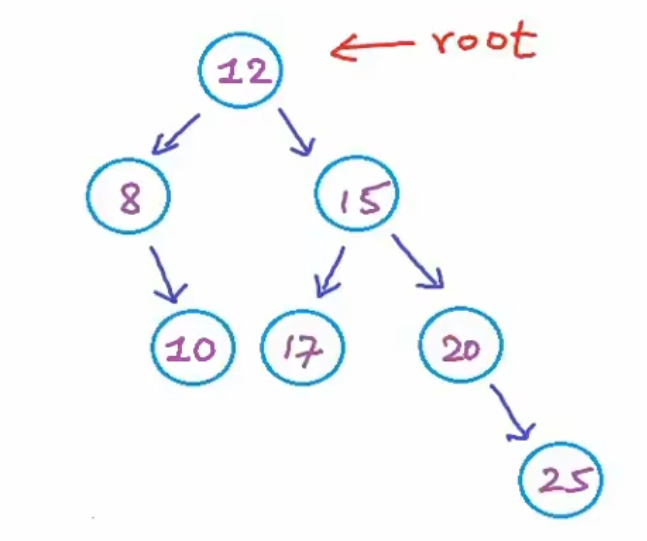
  • 对于下图这棵树来说它是一颗平衡的BST，因为对于所有节点来说，左右子树的高度差不大于1，但最好的情况仍然是完美二叉树的排列。

image-20250315160137675

Insert(x)

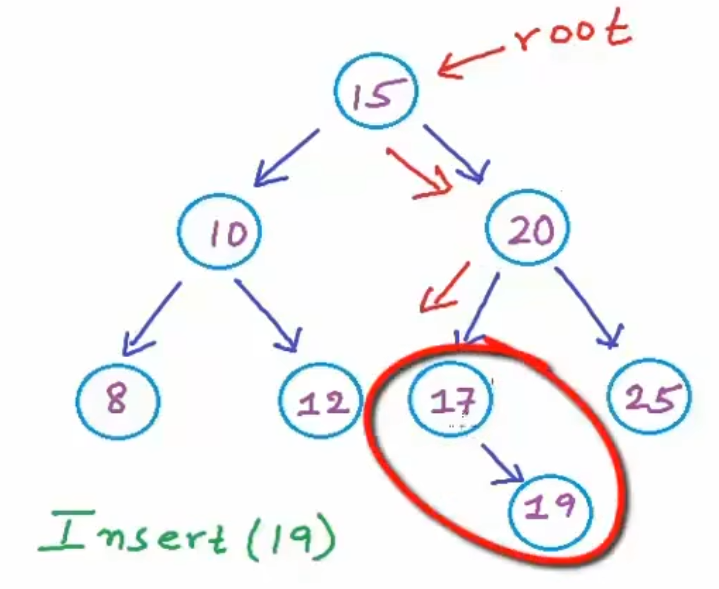
Insert(19)，与查找类似，从根节点开始进行比较，发现要插入的值更大，来到右子树，重复步骤，最后通过指针将节点链接起来，时间复杂度为$O(log_2^n)$

image-20250315160608243

Delete(x)

删除也同样类似，首先进行查找要删除的节点，将指针重新链接，需要注意的是在插入和删除节点的过程中会使得BST不在平衡，但有一些方法可以避免这种情况。