二叉树的概念

二叉树

  • 二叉树的唯一条件是每个节点最多只能有两个子节点（可以只有一个）
  • 没有子节点的节点被称为leaf node
  • 二叉树的唯一条件是一个节点不能有超过两个的子节点
  • 一个节点的深度定义为从根节点到该节点的路径长度
  • 第$i$层的最大节点数为 $2^i$
  • 二叉树的高度是从根到叶子的最长路径（边的数量），即只有一个节点的树高度为0，空树的高度为-1

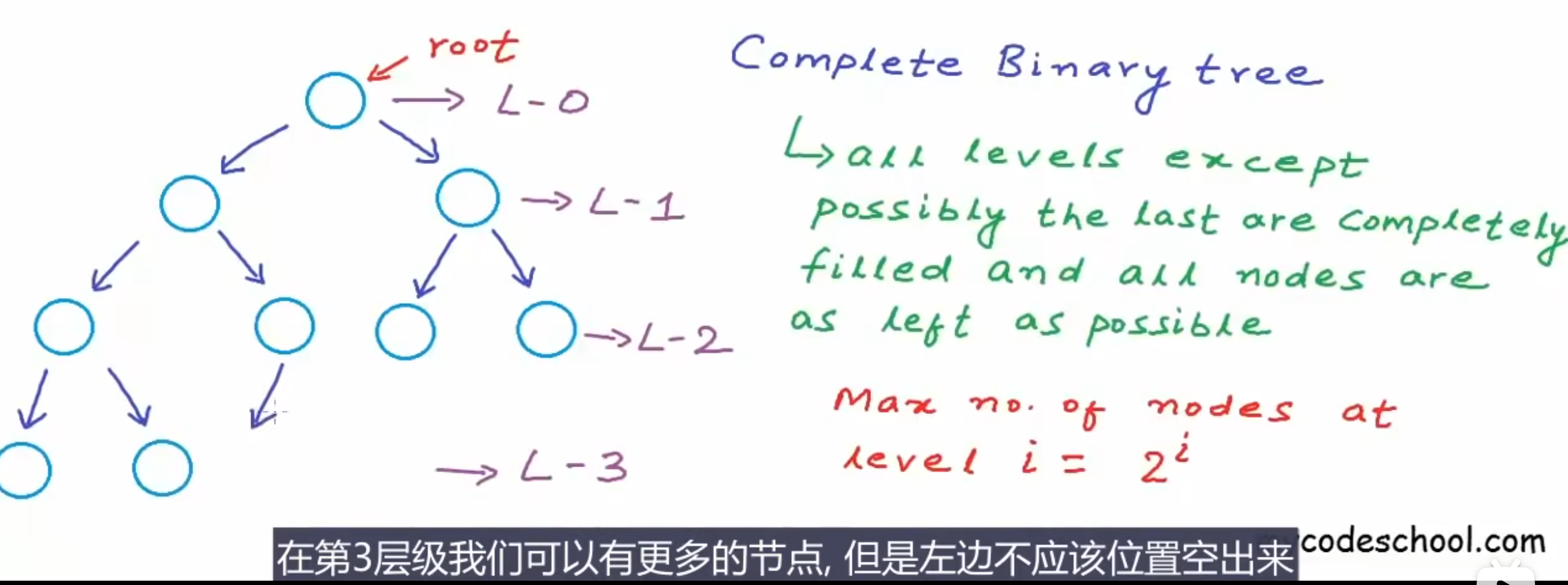
    树的类型

    Strict/Proper Binary Tree 严格二叉树

    each node can have either 0 or 2 children 每个节点只能有2个或0个子节点

    Complete Binary Tree 完全二叉树

    all level except possibly the last are completely filled and all nodes are left as possible(最后一层节点必须向左填充，其他层节点均填满)
    completeBinaryTree

    Perfect Binary Tree 完美二叉树

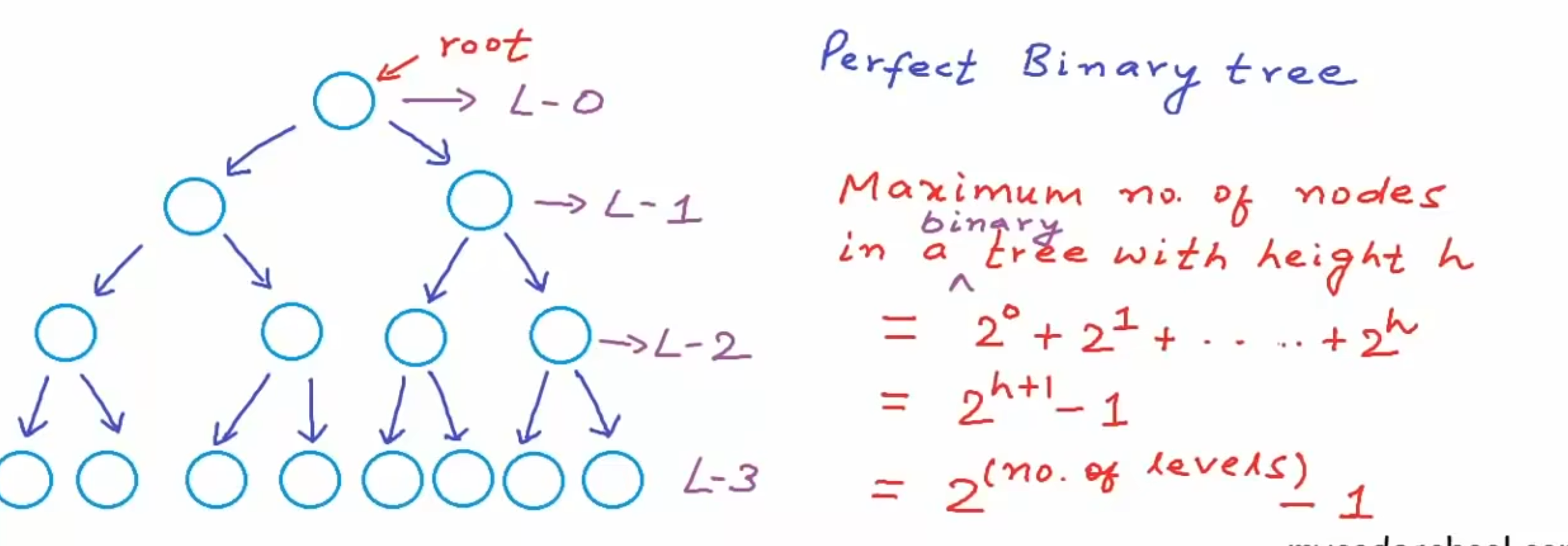
    all levels will be completely filled
    所有节点的数量为$2^{h+1}-1 = 2^{(numbers Of Levels)}-1$，h为高度，此处为3
    perfectBinaryTree
    n个节点的完美二叉树的高度是多少？
    $h = int(log_2^{n+1}-1)$
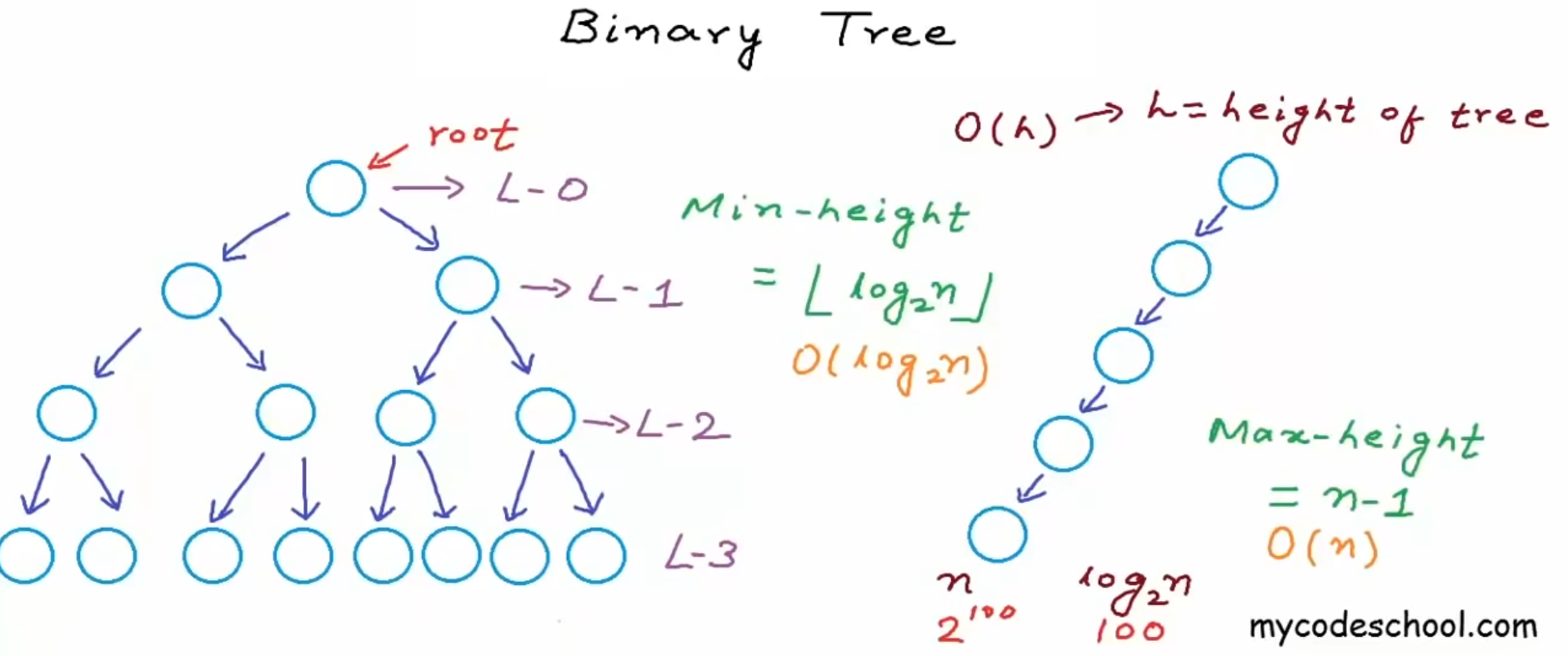
    Height of complete binary tree with n nodes n个节点的完全二叉树的高度为
    $h = log_2^n$
    很多操作的时间复杂度取决于树的高度，因此我们希望树的高度尽可能低，或者说保持二叉树尽可能平衡
    Height of the tree will be less if the tree will be dense,if the tree will be close to a perfect binary tree or complete binary tree（树如果较为密集的话书的高度就会相对较小，就会更为靠近完美或完全二叉树）
    对于一个完美二叉树或完全二叉树来说，时间复杂度将会是$O(log^n)$，n为节点数，对于sparse稀疏二二润茶叔，时间复杂度为$O(n)$，类似数组和链表
    timeCompelexity

    Balanced binary tree

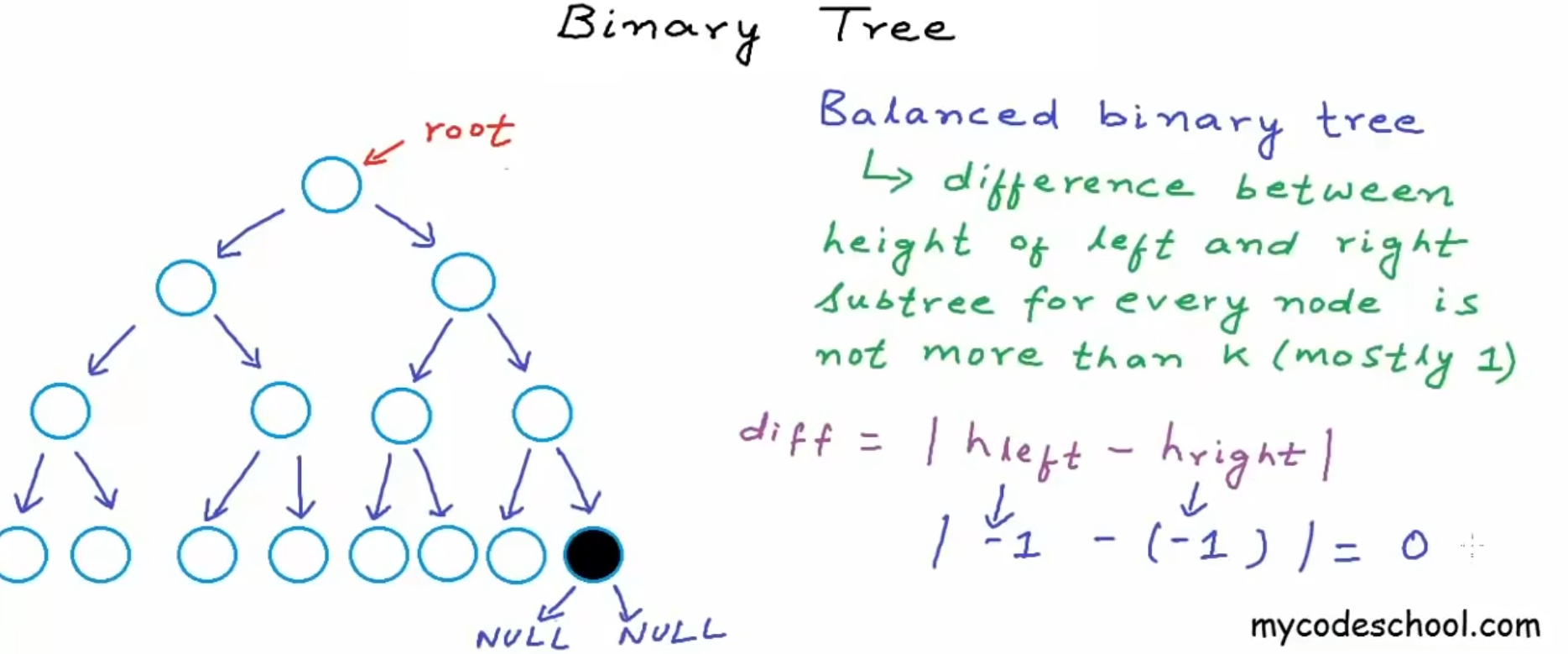
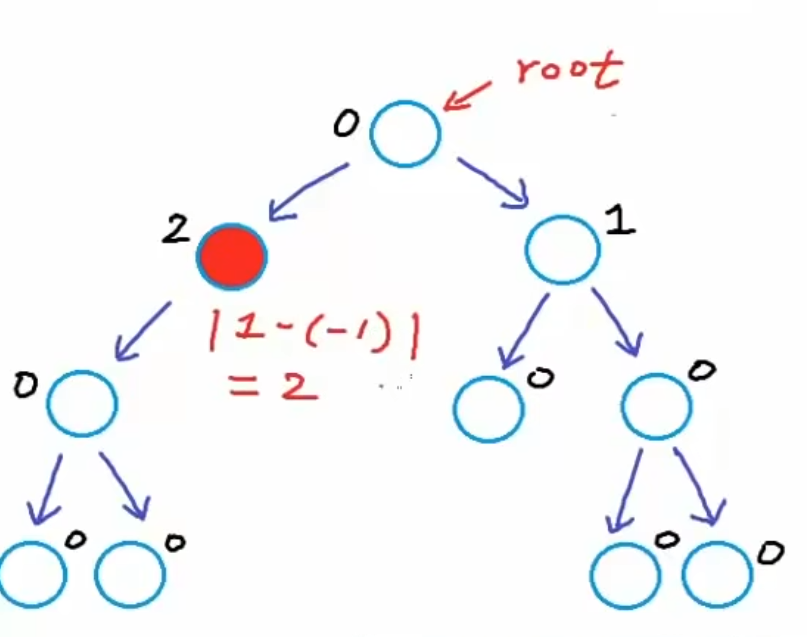
    对于每一个节点，左子树和右子树之间的高度不大于k，大多数时候k=1
    高度差 $diff = |hleft - hright|$
    heightDiff
    这里对于红色节点来说，左子树的高度是1，右子树为空，高度为-1，因此高度差为2
    image-20250314144337270
    二叉树的实现：
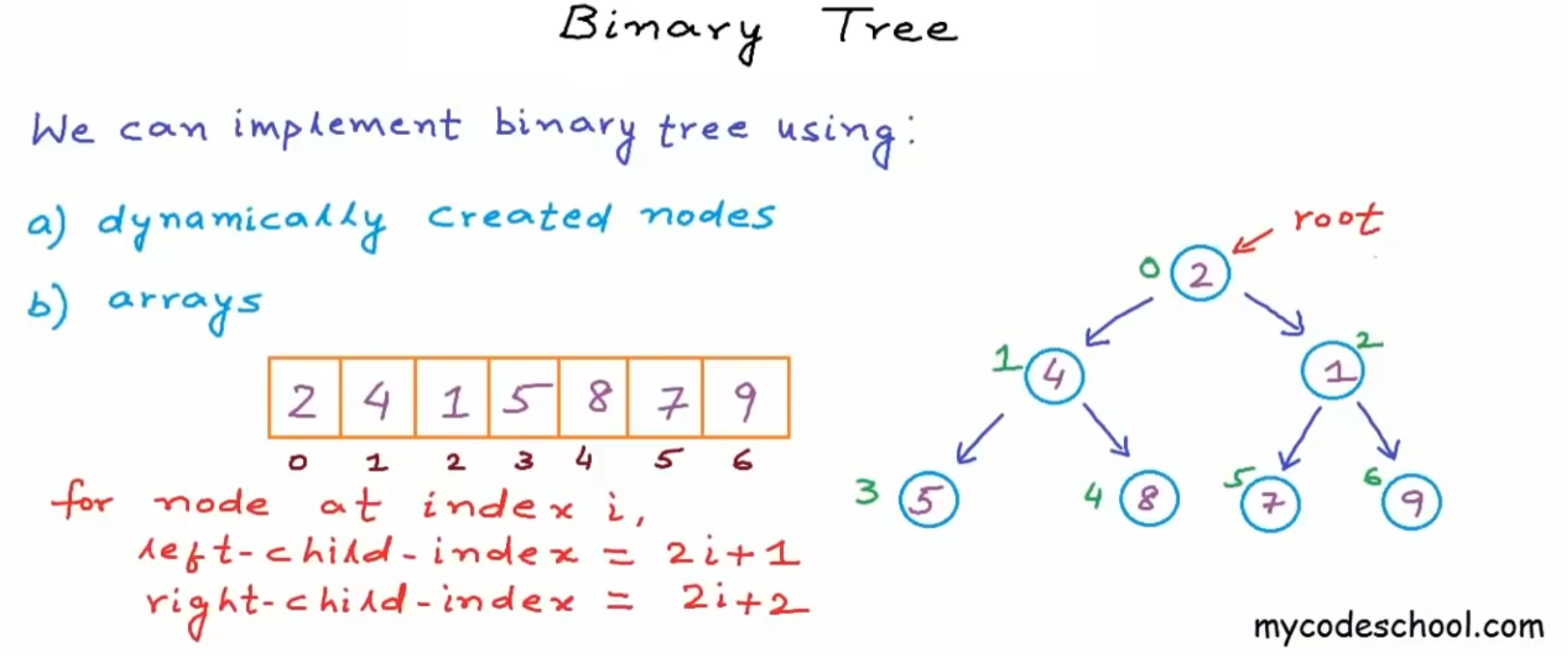
    a)链表：动态的创建节点，通过指针来链接
    b)数组（用heaps来实现）：常被用做complete binary tree，如下图绿色标号，从上到下从左到右依次编号索引 ，依次填入数组中
    对于一个在数组中索引为i的节点来说：
    左子节点的索引为$2i+1$，右子节点的索引为$2i+2$
    image-20250314200551008